Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
конъюнктивная нормальная форма (КНФ) -- конъюнкция нескольких дизъюнкций, например, $\left(A\vee \overline{B}\vee C\right)\wedge \left(A\vee C\right)$;
дизъюнктивная нормальная форма (ДНФ) -- дизъюнкция нескольких конъюнкций, например, $\left(A\wedge \overline{B}\wedge C\right)\vee \left(B\wedge C\right)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) -- это КНФ, удовлетворяющая трем условиям:
не содержит одинаковых элементарных дизъюнкций;
ни одна из дизъюнкций не содержит одинаковых переменных;
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) -- это ДНФ, удовлетворяющая трем условиям:
не содержит одинаковых элементарных конъюнкций;
ни одна из конъюнкций не содержит одинаковых переменных;
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
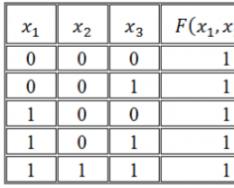
Записать логическую функцию по ее таблице истинности:
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
Рисунок 2.
Получим СДНФ:
Воспользуемся правилом построения СКНФ.
Дизъюнктивные и конъюнктивные нормальные формы алгебры высказываний. Для каждой функции логики высказываний можно составить таблицу истинности. Обратная задача тоже всегда разрешима. Введем несколько определений.
Элементарными конъюнкциями (конъюнктами) называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более
одного раза.
Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций.
Элементарными дизъюнкциями (дизъюнктами) называются дизъюнкции переменных с отрицаниями или без них.
Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции элементарных дизъюнкций.
Для каждой функции алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм.
Алгоритм построения ДНФ:
1. Перейти к булевым операциям, используя формулы эквивалентных преобразований.
2. Перейти к формулам с тесными отрицаниями, то есть к формуле, в которой отрицания располагаются не выше, чем над переменными – применить законы де Моргана.
3. Раскрыть скобки – применить законы дистрибутивности.
4. Повторяющиеся слагаемые взять по одному разу – закон идемпотентности.
5. Применить законы поглощения и полупоглощения.
Пример 6. Найти ДНФ формулы: .
В алгебре Буля справедлив принцип двойственности . Он заключается в следующем.
Функция называется двойственной к функции , если . Т.е. для нахождения функции, двойственной к заданной, необходимо построить отрицание функции от отрицаний аргументов.
Пример 7. Найти функцию, двойственную к .
Среди элементарных функций алгебры логики 1 двойственна 0 и наоборот, х двойственна х, двойственна , двойственна и наоборот.
Если в формуле F 1 представляющей функцию все конъюнкции заменить
на дизъюнкции, дизъюнкции на конъюнкции, 1 на 0, 0 на 1, то получим формулу F * , представляющую функцию * , двойственную .
Конъюнктивная нормальная форма (КНФ) – двойственное для ДНФ понятие, поэтому ее легко построить по схеме:
Пример 8. Найти КНФ формулы: .
Воспользовавшись результатом примера 6, имеем
Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы. В каждом из типов нормальных форм (дизъюнктивных и конъюнктивных) можно выделить класс совершенных форм СДНФ и СКНФ.
Совершенной элементарной конъюнкцией называется логическое произведение всех переменных с отрицанием или без них, причем, каждая переменная входит в произведение только один раз.
Всякую ДНФ можно привести к СДНФ расщеплением конъюнкций, которые содержат не все переменные, т.е. добавлением для отсутствующей переменной x i множится с применением закона дистрибутивности
Пример 9. Найти СДНФ для ДНФ примера 6
Совершенной элементарной дизъюнкцией называется логическая сумма всех переменных с отрицаниями или без них, причем, каждая переменная входит в сумму только один раз.
Всякую КНФ можно привести к СКНФ, добавляя член конъюнкции, не содержащий какой – либо переменной X i конъюнкцией и применяя дистрибутивный закон
Пример 10 . Привести КНФ к СКНФ:
Для построения СКНФ можно воспользоваться схемой
Пример 11. Найти СКНФ для формулы примера 6.
Всякая функция имеет СДНФ и, притом, единственную . Каждая функция имеет СКНФ и, притом, единственную .
Т.к. СДНФ и СКНФ определены формулами однозначно, их можно строить по таблице истинности формулы.
Для построения СДНФ необходимо выделить строки, в которых F принимает значение 1 и записать для них совершенные элементарные конъюнкции. Если значение переменной в нужной строке таблицы истинности равно единице, то в совершенном конъюнкте она берется без отрицания, если нулю – то с отрицанием. Затем совершенные конъюнкты (их число равно числу единиц в таблице) соединяются знаками дизъюнкции.
Для построения СКНФ по таблице истинности необходимо выделить в ней строки, где F=0, и записать совершенные элементарные дизъюнкции, после чего соединить их знаками конъюнкции. Если в требуемой строке таблицы истинности (F=0) значение переменной соответствует нулю, то в совершенном дизъюнкте она берется без отрицания, если единице – то с отрицанием.
Пример 12. Найти СДНФ и СКНФ по таблице истинности для формулы примера 6.
В таблице 14 приведено лишь конечное значение F=10101101. В справедливости этого утверждения следует убедиться самостоятельно, построив развернутую таблицу истинности.
Таблица 14
| x | y | z | ||
Простой дизъюнкцией { англ. inclusive disjunction } или дизъюнктом { англ. disjunct } называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая дизъюнкция
- полная , если в неё каждая переменная (или её отрицание) входит ровно один раз;
- монотонная , если она не содержит отрицаний переменных.
Конъюнктивная нормальная форма, КНФ { англ. conjunctive normal form, CNF } нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.
Пример КНФ: $f(x,y) = (x \lor y) \land (y \lor \neg { z })$
СКНФ
Совершенная конъюнктивная нормальная форма, СКНФ { англ. perfect conjunctive normal form, PCNF } - это такая КНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых дизъюнкций
- каждая простая дизъюнкция полная
Пример СКНФ: $f(x,y,z) = (x \lor \neg { y } \lor z) \land (x\lor y \lor \neg { z })$
Теорема: Для любой булевой функции $f(\vec { x })$, не равной тождественной единице, существует СКНФ, ее задающая.
Доказательство: Поскольку инверсия функции $\neg { f } (\vec x)$ равна единице на тех наборах, на которых $f(\vec x)$ равна нулю, то СДНФ для $\neg { f } (\vec x)$ можно записать следующим образом:
$\neg { f } (\vec x) = \bigvee\limits_ { f(x^ { \sigma_ { 1 } } , x^ { \sigma_ { 2 } } , ... ,x^ { \sigma_ { n } }) = 0 } (x_ { 1 } ^ { \sigma_ { 1 } } \wedge x_ { 2 } ^ { \sigma_ { 2 } } \wedge ... \wedge x_ { n } ^ { \sigma_ { n } }) $, где $ \sigma_ { i } $ обозначает наличие или отсутствие отрицание при $ x_ { i } $
Найдём инверсию левой и правой части выражения:
$ f(\vec x) = \neg ({ \bigvee\limits_ { f(x^ { \sigma_ { 1 } } , x^ { \sigma_ { 2 } } , ... ,x^ { \sigma_ { n } }) = 0 } (x_ { 1 } ^ { \sigma_ { 1 } } \wedge x_ { 2 } ^ { \sigma_ { 2 } } \wedge ... \wedge x_ { n } ^ { \sigma_ { n } }) }) $
Применяя дважды к полученному в правой части выражению правило де Моргана, получаем: $ f(\vec x) = \bigwedge \limits_ { f(x^ { \sigma_1 } , x^ { \sigma_2 } , \dots ,x^ { \sigma_n }) = 0 } $ $(\neg { x_1^ { \sigma_1 } } \vee \neg { x_2^ { \sigma_2 } } \vee \dots \vee \neg { x_n^ { \sigma_n } }) $
Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая может быть построена для любой функции, не равной тождественному нулю, то теорема доказана.
Алгоритм построения СКНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно $0$.
- Для каждого отмеченного набора записываем дизъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть $0$, то в дизъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные дизъюнкции связываем операциями конъюнкции.
Пример построения СКНФ для медианы
1). В таблице истинности отмечаем те наборы переменных, на которых значение функции равно $0$.
| x | y | z | $ \langle x,y,z \rangle $ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2). Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть $0$, то в дизъюнкцию включаем саму переменную, иначе ее отрицание.
| x | y | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | $(x \lor y \lor z)$ |
| 0 | 0 | 1 | 0 | $(x \lor y \lor \neg { z })$ |
| 0 | 1 | 0 | 0 | $(x \lor \neg { y } \lor z)$ |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | $(\neg { x } \lor y \lor z)$ |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3). Все полученные дизъюнкции связываем операциями конъюнкции.
$ \langle x,y,z \rangle = (x \lor y \lor z) \land (\neg { x } \lor y \lor z) \land (x \lor \neg { y } \lor z) \land (x \lor y \lor \neg { z })$
Примеры СКНФ для некоторых функций
Стрелка Пирса: $ x \downarrow y = (\neg { x } \lor { y }) \land ({ x } \lor \neg { y }) \land (\neg { x } \lor \neg { y }) $
Исключающее или: $ x \oplus y \oplus z = (\neg { x } \lor \neg { y } \lor z) \land (\neg { x } \lor y \lor \neg { z }) \land (x \lor \neg { y } \lor \neg { z }) \land (x \lor y \lor z)$
Простой конъюнкцией называется конъюнкция одной или нескольких переменных , при этом каждая переменная встречается не более одного раза (либо сама , либо ее отрицание ).
Например, является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций .
Например, выражение является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма , у которой в каждую конъюнкцию входят все переменные данного списка (либо сами , либо их отрицания ), причем в одном и том же порядке .
Например, выражение является ДНФ, но не СДНФ. Выражение 
является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных , при этом каждая переменная входит не более одного раза (либо сама , либо ее отрицание ).Например, выражение - простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение - КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение 
является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
Если среди дизъюнктных слагаемых в ДНФ имеются слагаемые 
, то ко всей дизъюнкции добавляем слагаемое К
1 К
2 . Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
Если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ 
, после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z , вставляем в нее выражение ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z , то добавляем в нее выражение (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Конъюнктивная нормальная форма удобна для автоматического доказательства теорем . Любая булева формула может быть приведена к КНФ. Для этого можно использовать: закон двойного отрицания , закон де Моргана , дистрибутивность .
Энциклопедичный YouTube
-
1 / 5
Формулы в КНФ :
¬ A ∧ (B ∨ C) , {\displaystyle \neg A\wedge (B\vee C),} (A ∨ B) ∧ (¬ B ∨ C ∨ ¬ D) ∧ (D ∨ ¬ E) , {\displaystyle (A\vee B)\wedge (\neg B\vee C\vee \neg D)\wedge (D\vee \neg E),} A ∧ B . {\displaystyle A\wedge B.}Формулы не в КНФ :
¬ (B ∨ C) , {\displaystyle \neg (B\vee C),} (A ∧ B) ∨ C , {\displaystyle (A\wedge B)\vee C,} A ∧ (B ∨ (D ∧ E)) . {\displaystyle A\wedge (B\vee (D\wedge E)).}Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:
¬ B ∧ ¬ C , {\displaystyle \neg B\wedge \neg C,} (A ∨ C) ∧ (B ∨ C) , {\displaystyle (A\vee C)\wedge (B\vee C),} A ∧ (B ∨ D) ∧ (B ∨ E) . {\displaystyle A\wedge (B\vee D)\wedge (B\vee E).}Построение КНФ
Алгоритм построения КНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
A → B = ¬ A ∨ B , {\displaystyle A\rightarrow B=\neg A\vee B,} A ↔ B = (¬ A ∨ B) ∧ (A ∨ ¬ B) . {\displaystyle A\leftrightarrow B=(\neg A\vee B)\wedge (A\vee \neg B).}2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
¬ (A ∨ B) = ¬ A ∧ ¬ B , {\displaystyle \neg (A\vee B)=\neg A\wedge \neg B,} ¬ (A ∧ B) = ¬ A ∨ ¬ B . {\displaystyle \neg (A\wedge B)=\neg A\vee \neg B.}3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения КНФ
Приведем к КНФ формулу
F = (X → Y) ∧ ((¬ Y → Z) → ¬ X) . {\displaystyle F=(X\rightarrow Y)\wedge ((\neg Y\rightarrow Z)\rightarrow \neg X).}Преобразуем формулу F {\displaystyle F} к формуле, не содержащей → {\displaystyle \rightarrow } :
F = (¬ X ∨ Y) ∧ (¬ (¬ Y → Z) ∨ ¬ X) = (¬ X ∨ Y) ∧ (¬ (¬ ¬ Y ∨ Z) ∨ ¬ X) . {\displaystyle F=(\neg X\vee Y)\wedge (\neg (\neg Y\rightarrow Z)\vee \neg X)=(\neg X\vee Y)\wedge (\neg (\neg \neg Y\vee Z)\vee \neg X).}В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
F = (¬ X ∨ Y) ∧ ((¬ Y ∧ ¬ Z) ∨ ¬ X) . {\displaystyle F=(\neg X\vee Y)\wedge ((\neg Y\wedge \neg Z)\vee \neg X).}Например, следующая формула записана в 2-КНФ:
(A ∨ B) ∧ (¬ B ∨ C) ∧ (B ∨ ¬ C) . {\displaystyle (A\lor B)\land (\neg B\lor C)\land (B\lor \neg C).} Коэффициенты
